刘维尔定理为什么是物理学中的重要数学工具
大家好呀!今天想和大家聊聊一个听起来有点高大上但实际上超级实用的数学工具——刘维尔定理。作为一个经常在物理和数学之间来回切换的小编,我发现这个定理简直是连接两个领域的"万能胶",特别有意思!
刘维尔定理是个啥?
首先得说说这个定理到底是什么。简单来说,刘维尔定理告诉我们:在哈密顿力学系统中,相空间体积在时间演化过程中保持不变。啥?听不懂?别急,让我用更接地气的话解释一下。
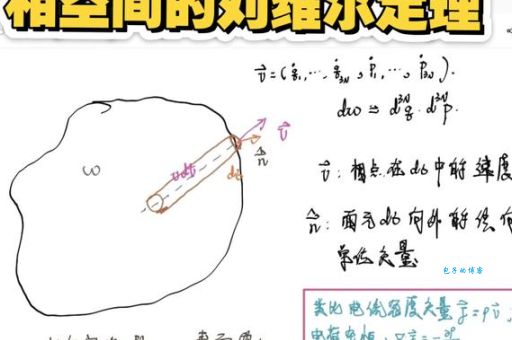
想象你有一团气球,里面装满了代表系统状态的"小点点"。随着时间推移,这团气球可能会被拉长、压扁、扭曲,但神奇的是,它的总体积永远不会改变!这就是刘维尔定理的精髓所在。
我次接触这个定理时,觉得它简直像变魔术一样神奇。明明系统在变化,相空间体积却能保持不变,这不科学啊!但后来发现,正是这种"不变性"让它成为了物理学中的超级工具。
为什么物理学家爱死它了?
物理学家们对刘维尔定理的热爱程度,简直像我对奶茶的依赖一样深。为什么呢?因为它解决了几个关键
1. 统计力学的基石:没有它,我们可能到现在还搞不清楚热力学和微观世界的关系。它让统计力学有了坚实的数学基础。
2. 保真度保证:在模拟物理系统时,刘维尔定理保证了数值计算的可靠性,就像给计算过程上了一样。
3. 简化复杂很多看似复杂的利用这个定理可以大大简化,简直是物理学家的"懒人包"。
记得我次用这个定理解决实际问题时,那种"哇,原来可以这么简单!"的感觉至今难忘。它就像一把瑞士军刀,看起来简单,但功能强大得惊人。
实际应用中的"魔法"
让我们看看刘维尔定理在实际中的几个"魔法"应用:
| 应用领域 | 作用 | 重要性 |
|---|---|---|
| 统计力学 | 建立微观状态与宏观量的联系 | 基础性 |
| 天体力学 | 研究多体系统长期演化 | 关键性 |
| 量子力学 | 连接经典与量子描述 | 桥梁作用 |
| 流体力学 | 描述无粘性流体运动 | 理论支撑 |
看到没?从微观世界到浩瀚宇宙,这个定理无处不在。我喜欢的是它在混沌系统中的应用——即使系统变得完全不可预测,相空间体积依然保持不变,这种"混乱中的秩序"简直太酷了!
为什么学物理的都得懂它?
作为一个过来人,我强烈建议每个学物理的同学都要好好掌握刘维尔定理。为什么呢?
它是连接经典力学和统计力学的关键。没有它,统计力学中的很多概念就像没有地基的房子,摇摇欲坠。
它提供了一种思考物理问题的新视角。掌握了它,你看待物理系统的眼光会完全不同,就像突然获得了一副X光眼镜一样。
它实在是太有用了!从期末考试到科研工作,这个定理会反复出现,成为你的"救命稻草"。我至少有三四次靠它解决了看似无解的
我的"顿悟"时刻
记得有一次在研究分子动力学模拟时,我完全搞不明白为什么某些算法能够保持能量守恒。直到重新审视刘维尔定理,才恍然大悟——原来那些算法设计时就有意保持了相空间体积不变!那一刻的"顿悟"感,就像拼图后一块终于归位一样爽快。
这种经历让我明白,数学工具不只是冷冰冰的公式,而是理解物理世界的"解码器"。刘维尔定理尤其如此,它把复杂的动力学行为浓缩成了一个简洁而强大的原理。
给初学者的建议
如果你刚开始接触刘维尔定理,可能会觉得有点抽象。别担心,我当初也一样!以下是我总结的几个学习小技巧:
1. 多画图:相空间的概念很抽象,画出来会直观很多。我当初画了无数个变形但不改变体积的"相空间泡泡"。
2. 联系实际:找一些简单力学系统的例子,比如谐振子,亲自验证定理的正确性。
3. 循序渐进:先理解经典版本,再扩展到统计力学和量子力学中的应用。
4. 多问为什么:这个定理为什么成立?假设不成立会怎样?这种思考能加深理解。
记住,理解刘维尔定理不是一蹴而就的。我大概花了三个月才真正"get"到它的妙处,但一旦理解了,就会觉得它简直无处不在!
不变中的万变
刘维尔定理吸引我的地方在于它揭示了物理学中一个深刻的真理:在复杂的变化中,往往隐藏着简单的不变性。这种"不变中的万变"思想,不仅适用于物理系统,某种程度上也是理解世界的智慧。
每次想到这个19世纪就发现的定理至今仍在前沿的物理研究中发挥作用,我就感到特别兴奋。它就像一座跨越时空的桥梁,连接着经典与现代,简单与复杂。
那么,你在学习或研究中有没有遇到过让你"顿悟"的数学工具呢?或者你对刘维尔定理有什么独特的理解?欢迎分享你的故事和见解!