弧度单位与角度转换:实用公式和计算示例
大家好!今天我想和大家聊聊弧度与角度之间的转换,这个话题听起来可能有点数学味太重,但其实掌握了方法后,你会发现它其实挺简单的。作为一个曾经也为这个转换头疼过的人,我完全理解大家可能会遇到的困惑,所以我会尽量用轻松的方式来解释。
为什么我们需要弧度?
记得我刚开始学三角数的时候,脑子里全是问号:为什么有了角度还要搞出个弧度来?这不是给自己找麻烦吗?后来才明白,弧度其实在很多情况下比角度更方便,特别是在高等数学和物理学中。
弧度大的优点就是它直接与圆的半径和弧长相关。1弧度定义为弧长等于半径时所对应的圆心角。这种定义方式让很多公式变得特别简洁,比如著名的弧长公式:弧长=半径×圆心角(弧度)。如果使用角度制,这个公式就得加上一个π/180的系数,多麻烦啊!
基本概念:角度与弧度的关系
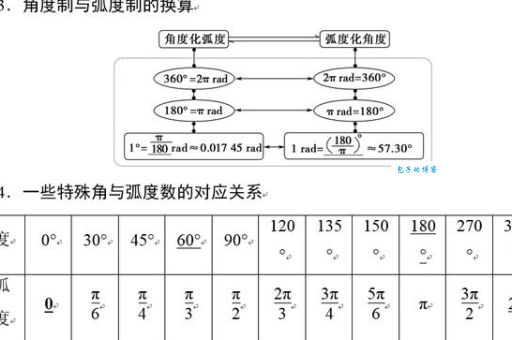
让我们先搞清楚基本的关系:一个完整的圆周是360度,用弧度表示就是2π。所以:
360° = 2π 弧度

这个等式就是转换的基础。从这里我们可以推导出:
1° = π/180 弧度 ≈ 0.0174533 弧度
1 弧度 = 180°/π ≈ 57.2958°
是不是看起来很简单?记住这两个基本关系,大部分转换问题都能解决了。
实用转换公式
基于上面的基本关系,我们可以总结出两个超级实用的转换公式:
1. 角度转弧度公式:
弧度 = 角度 × (π/180)
2. 弧度转角度公式:
角度 = 弧度 × (180/π)
为了让大家更直观地理解,我整理了一个常见角度与弧度的对应表:
| 角度 | 弧度 | 精确值 | 近似值 |
|---|---|---|---|
| 0° | - - -|||
| 30° | π/6 | 0.5236 | ≈0.52 |
| 45° | π/4 | 0.7854 | ≈0.79 |
| 60° | π/3 | 1.0472 | ≈1.05 |
| 90° | π/2 | 1.5708 | ≈1.57 |
| 180° | π | 3.1416 | ≈3.14 |
| 270° | 3π/2 | 4.7124 | ≈4.71 |
| 360° | 2π | 6.2832 | ≈6.28 |
记住这个表格中的常见对应关系,能帮你省下不少计算时间!
计算示例:手把手教你转换
示例1:将45°转换为弧度
按照我们的公式:
弧度 = 角度 × (π/180)
所以:
45° × (π/180) = π/4 ≈ 0.7854 弧度
示例2:将π/3弧度转换为角度
角度 = 弧度 × (180/π)
所以:
(π/3) × (180/π) = 180/3 = 60°
示例3:将1.5弧度转换为角度
1.5 × (180/π) ≈ 1.5 × 57.2958° ≈ 85.9437°
示例4:将200°转换为弧度
200 × (π/180) = (10π)/9 ≈ 3.4907 弧度
看到没?其实转换起来真的不难,关键是要记住那两个基本公式。
为什么π这么重要?
在弧度制中,π无处不在。这是因为π代表了半圆的弧度值(180°)。很多同学可能会问:"为什么非要用π呢?用3.14不行吗?"其实在精确计算时,我们通常会保留π的符号形式,只有在需要数值结果时才进行近似计算。这样可以避免精度损失,也让表达式更简洁。
比如,sin(π/6)我们知道等于0.5,但如果用近似值3.1416/6≈0.5236来计算sin(0.5236),虽然结果也是0.5,但过程就复杂多了。
计算器使用小技巧
现在的科学计算器都有角度和弧度两种模式。在使用前一定要确认计算器当前处于哪种模式,否则计算结果会完全错误!我曾经就犯过这个错误,花了好久才找到问题所在。
角度模式(DEG):适用于角度计算
弧度模式(RAD):适用于弧度计算
比如你想计算sin(π/6),如果计算器在角度模式下,你输入sin(π÷6),得到的结果会是sin(30°)=0.5,这是正确的。但如果计算器在弧度模式下,你输入sin(30),计算的是sin(30弧度)≈-0.988,这就完全不对了。
常见误区与注意事项
1. 不要混淆π和180°:虽然π弧度等于180°,但它们不是同一个概念。π是一个无理数,约等于3.1416,而180是一个角度值。
2. 单位不要省略:在书写时,角度通常用度符号"°"表示,而弧度可以写"rad"或省略。但为了避免混淆,初学者好都写上单位。
3. 三角数参数的单位:在使用sin、cos等三角数时,一定要明确参数是角度还是弧度。Excel中默认使用弧度,而很多计算器默认使用角度,这点要特别注意。
4. 近似值的精度:π的近似值3.14在大多数情况下够用,但在需要高精度计算时,应该使用更多位数的π值或保留π的符号形式。
实际应用场景
弧度制在物理学和工程学中应用广泛,特别是在描述周期性现象时:
1. 简谐运动:x = A sin(ωt + φ),其中ω是角频率,单位为弧度/秒
2. 交流电路:电压和电流的相位差通常用弧度表示
3. 圆周运动:角速度通常用弧度/秒表示
在这些领域中,使用弧度能让公式更简洁,计算更方便。
记忆小窍门
刚开始学习时,我总是记不住角度和弧度的转换关系。后来我发现了一个记忆方法:想象一个半圆(180°),它对应的弧度是π。这样,当你需要转换时,可以想"180°对应π",然后按比例计算。
比如90°是180°的一半,所以弧度也是π的一半,即π/2。60°是180°的三分之一,所以弧度是π/3。这个方法对于常见角度的转换特别有用。
练习时间
为了帮助大家巩固所学,我准备了几道练习题,大家可以试着做做看:
1. 将120°转换为弧度(精确值和近似值)
2. 将5π/6弧度转换为角度
3. 计算sin(π/4)和cos(π/3)的值
4. 将2.5弧度转换为角度(保留两位小数)
(答案:1. 2π/3 ≈ 2.0944;2. 150°;3. √2/2 ≈ 0.7071和0.5;4. ≈143.24°)
结语
弧度与角度的转换其实就像两种语言之间的翻译,一旦掌握了基本规则,剩下的就是熟练度的问题了。希望这篇文章能帮你消除对弧度制的恐惧,让你在面对相关问题时能更加从容。
你次接触弧度制是什么时候?有没有什么特别的记忆或技巧想和大家分享?或者在学习过程中遇到过什么有趣的故事?欢迎在评论区聊聊你的经历!