柯西中值定理怎么用?看完这篇就懂了
大家好呀!今天咱们来聊聊数学分析里一个特别有意思的定理——柯西中值定理。我知道很多人一听到"中值定理"四个字就开始头疼,但别担心,我会用轻松的方式带你理解它,保证你看完这篇文章就能明白怎么用!
先说说这个定理是啥
柯西中值定理是拉格朗日中值定理的升级版,简单来说就是:如果两个数在闭区间[a,b]上连续,在开区间(a,b)内可导,而且g'(x)在这个区间内不等于0,那么至少存在一点c∈(a,b),使得:

[f(b)-f(a)]/[g(b)-g(a)] = f'(c)/g'(c)
看不懂?没关系!咱们用大白话解释一下:想象你和朋友一起跑步,你跑的距离是f(t),朋友跑的距离是g(t)。柯西中值定理就是说,在某个时刻,你们俩的瞬时速度比等于全程的平均速度比。
这个定理有啥用?
柯西中值定理在数学分析中特别重要,它能帮我们:
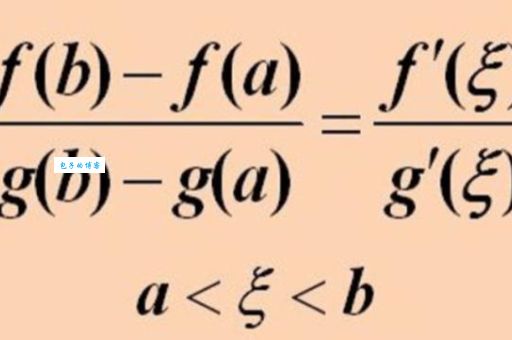
1. 证明一些重要的数学结论
2. 解决某些极限 推导其他定理(比如洛必达法则)
4. 分析数的性质
| 场景 | 柯西中值定理的应用 |
|---|---|
| 证明不等式 | 通过构造适当的数,用柯西中值定理建立关系 |
| 求极限 | 特别是0/0或∞/∞型不定式极限 |
| 数分析 | 研究数的变化率之间的关系 |
怎么用?来看几个例子
例子1:证明不等式
假设我们要证明:对于0 我们可以设f(x)=lnx,g(x)=x,在[a,b]上应用柯西中值定理: 存在c∈(a,b),使得(lnb-lna)/(b-a)=1/c 因为a 例子2:推导洛必达法则 柯西中值定理是洛必达法则的基础。当遇到0/0型极限时,我们可以构造两个数,用柯西中值定理把数比转化为导数比,这样就容易求极限了。 使用时的注意事项 1. 条件检查:一定要确认数在闭区间连续,开区间可导,且g'(x)≠0 2. 数选择:要根据问题特点选择合适的f(x)和g(x) 3. 结论理解:c点的位置通常不知道,但知道它存在就够了 4. 与其他定理区分:不要和拉格朗日中值定理混淆 常见误区 很多同学刚开始用柯西中值定理时容易犯这些错误: 1. 忘记检查g'(x)≠0的条件 2. 把f和g的顺序搞反了 3. 以为c点是唯一的(其实可能有多个) 4. 在g(b)=g(a)的情况下还强行使用 实际应用小技巧 1. 遇到两个数比值的考虑柯西中值定理 2. 证明涉及两个数差值的不等式时,柯西中值定理可能有用 3. 当拉格朗日中值定理不够用时,升级到柯西中值定理 4. 记住标准形式,但也要灵活变形应用 为什么这个定理重要? 柯西中值定理架起了数值与导数值之间的桥梁。它不像拉格朗日中值定理只关注一个数,而是研究两个数之间的关系,这使得它在处理更复杂的问题时特别有用。 在物理中,它可以用来描述两个相关量的变化率关系;在经济学中,可以分析两个经济指标之间的动态关系;在工程中,能帮助理解系统参数之间的相互影响。 总结一下 柯西中值定理虽然看起来有点抽象,但一旦掌握了它的使用方法和适用场景,就会成为你数学工具箱中的一件利器。记住它的三个关键点: 1. 两个数都要满足连续和可导条件 2. 分母数的导数不能为零 3. 结论建立了平均变化率与瞬时变化率之间的联系 下次当你遇到两个数比值的问题时,不妨想想柯西中值定理,说不定就能迎刃而解啦! 你在学习柯西中值定理时遇到过哪些困难?或者你有什么特别好的记忆方法吗?欢迎在评论区分享你的经验,让我们一起探讨这个有趣的数学定理!